-
ログイン
-
スタディサプリENGLISHを
スタディサプリで学習するためのアカウント
学習Webにログインご契約情報を管理するためのアカウント
サポートWebにログイン(保護者の方はこちら)
ご利用の方はこちら
-
- 会員登録
間違えたところを忘れるころに再出題苦手克服定期テストもバッチリ!
9 教科受け放題 月額 2,178\~
ベーシックコース1か月無料キャンペーン 期間| 2024/4/1 (月) 0:00 ~ 2024/4/25 (木) 16:59 まで
クレジットカード決済限定
※コンビニ決済、App Store決済、Google Play Store決済でのお申し込みは対象外です。
14日間以内に利用停止手続きをすれば料金は一切不要!
申し込めばすぐ授業視聴可能です
※ 14日間には「受講申し込み日」を含みます。
※ 14日間無料体験はWebサイト、かつクレジットカード決済での受講申し込み手続きをされた場合のみに適用されます。
スタディサプリは
9教科受け放題※ 映像授業は5教科・演習問題は実技を含めた9教科に対応

演習1万問解き放題

※ 2022年6月時点
お子さまの個性に合わせて選べる 2つのコース
ベーシックコース
こんな方におすすめ!
- 通信教育と
お悩みの方 - 自分のペースで
勉強したい - 月々の負担を
減らしたい
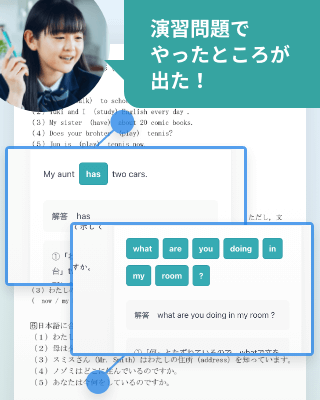
厳選予想問題で
定期テスト対策
ミッション機能で
迷わず学習
個別指導塾オンライン
こんな方におすすめ!
- 個別に指導して
もらたい - 質問や相談が
したい - 塾とお悩みの方
ベーシックコースの特長
実技教科も対応!
短期間で苦手科目も高得点が狙える
9教科対応の定期テスト対策
定期テスト対策は英数国理社に加え、実技4教科(音楽・美術・技術家庭・保健体育)も対応!
厳選予想問題で
実際のテストに近い形式で演習ができる
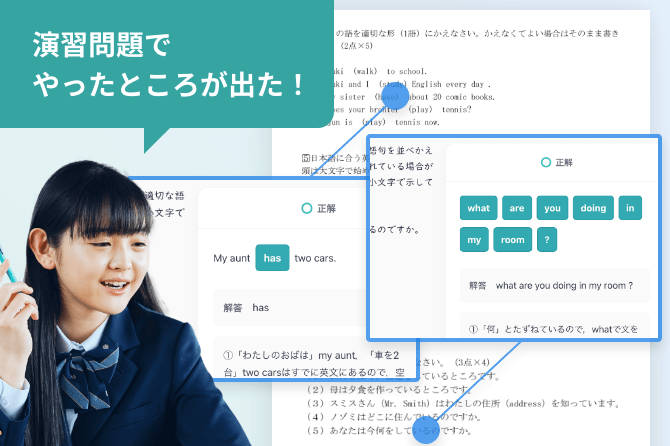
※ 画面はイメージです。画像内のテストは実際の定期テストではありません
教科書に対応した定期テスト厳選予想問題は、テストに出やすい問題からテストで差がつく応用問題までを収録。問題が厳選されているから短時間で効率的に学習できます。選択式だけでなく記述式や語句を解答する問題が出題されるので、実際の定期テストに近い実戦的な演習問題になっています。
また、テストで点差がつきやすい英作文問題や英語の教科書本文以外の長文問題の出題、数学の難問の出題もあるので、高得点を目指すことができます。
徹底暗記マスターで
スキマ時間にサクサク学習!
手軽に暗記できる

暗記マスターはテストに出やすい語句を厳選。手軽に暗記の学習ができます。
※ 暗記マスターには数学と国語はありません
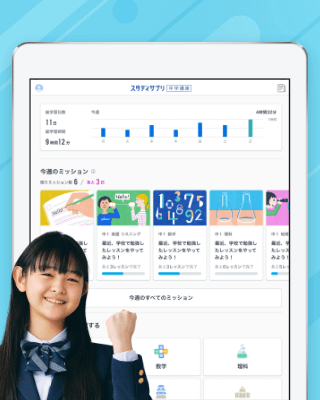
ミッション機能で
いつから何を始めればよいかわかる
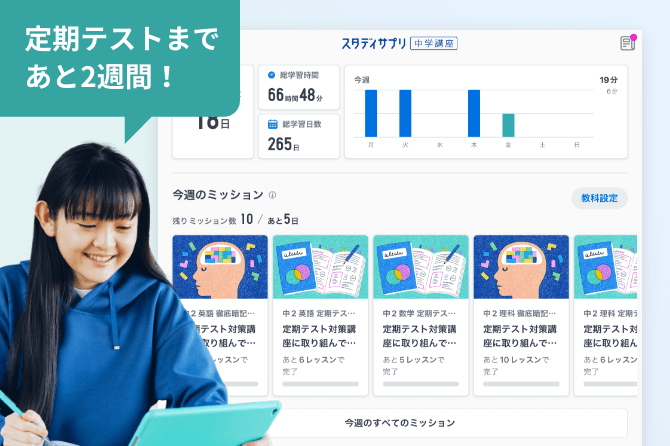
定期テストの日程を入力すれば、テスト時期が近付くと「今週のミッション」で提案してくれるので、ミッションにアクセスするだけで迷わず学習を開始できます。
お子さまはどちらのタイプ?
- 部活や習い事に忙しいから
効率よく定期テストの
勉強をしたい! - 定期テスト厳選予想問題のミッションをやりきりましょう。テストに出やすい問題を厳選しているので効率的に対策に取り組めます。
- 定期テストでは高得点を
目指したいから
どんどんチャレンジしたい! - 定期テスト厳選予想問題の基本問題からさらに難易度の高い問題へチャレンジ。高得点を目指しましょう。
※英・数・理・社対応
点数アップのうれしい声が続々! 利用者の声
スタディサプリ中学講座で
点数アップを
目指せる理由
理由01
苦手を徹底くり返し ミッション機能で反復学習
理由02
中学3年分を網羅 1万問以上の演習問題
理由03
ミッション機能で迷わない 今週やるべき学習をお知らせ
理由04
1回5分で集中が途切れない 厳選講師陣による神授業
理由05
苦手をつぶす・得意を伸ばす 戻り学習・先取り学習
中学講座のアプリ/Webブラウザについて
※ 中学講座では中学講座専用のアプリ「スタディサプリ中学講座」を利用しますので、小学講座・高校講座で「スタディサプリ 小学/中学/高校/大学受験講座」を利用いただいていた方は、専用アプリをダウンロードください。(追加料金などはかかりませんのでご安心ください)
※ Webブラウザも小学・高校講座のものと異なりますので、表示を確認の上、ご利用ください。(ログイン後、中学生の方は自動的に中学講座専用のWebブラウザにアクセスされます)
学校向けサービスと個人向けサービスの違いについて
※ 本ページで説明している個人向けサービスと学校向けサービスとでは提供するサービス内容が異なります。家庭学習は新機能を含む個人向けサービスのご利用がおすすめです。
サービスの違いについての詳細はこちらをご参照ください。
理由01
苦手を徹底くり返し ミッション機能で反復学習
苦手をつぶすには
理解するまでくり返すことが大切です
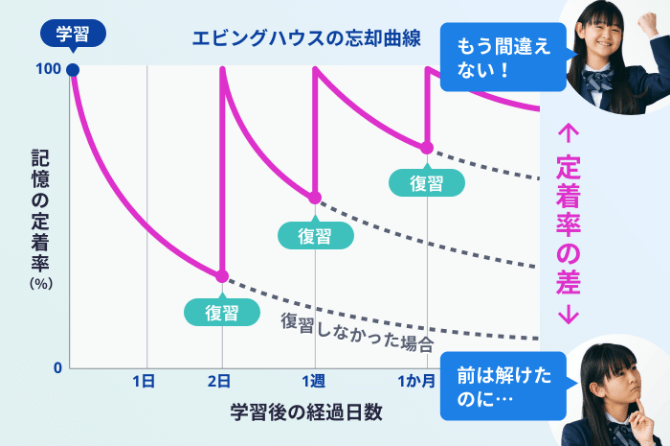
「習った時はわかったはずの問題も、もう一度解こうとしたら間違えてしまった…」ということはありませんか?理解し、知識として定着させるには繰り返しが重要です。
間違えたところを
忘れた頃に再出題します
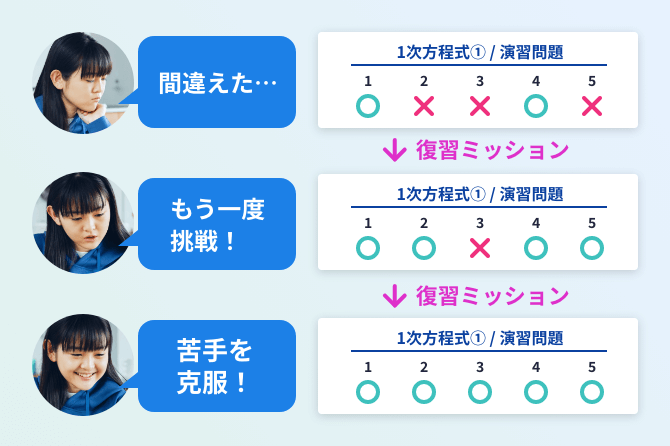
学習履歴にもとづいて間違えた単元の解き直しを提案する復習ミッションを搭載。
一定期間ごとに提示して知識の定着を図ります。
理由02
中学3年分を網羅 1万問以上の演習問題
豊富な演習問題で
お子さまの理解度に合わせた学習が可能です
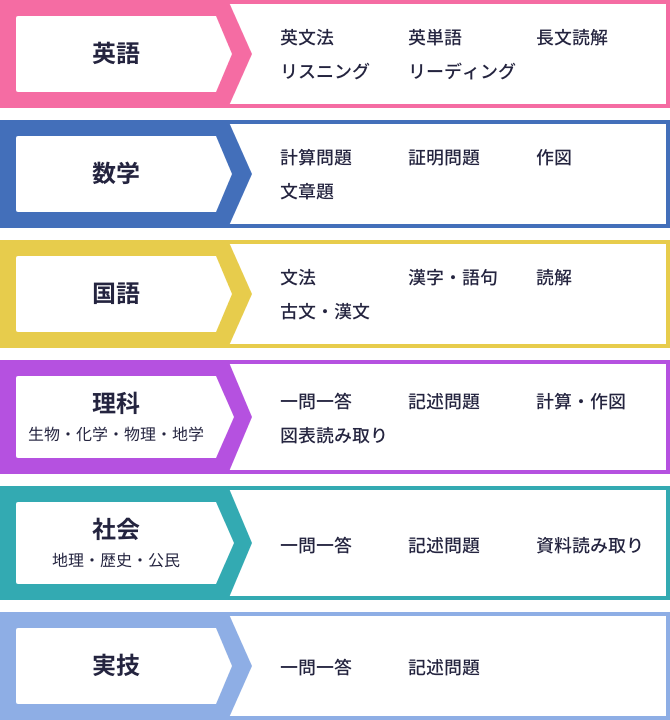
演習問題は、9教科約1万問以上も収録しています。授業動画で理解した内容を、演習問題により確認することで、学習した内容をしっかり定着させます。
演習問題は自動採点・ポイント解説付

タブレットやスマホで授業を視聴した後は、演習問題を解いて学習内容を確認します。演習は自動採点なので、お子さまひとりでも問題ありません。間違えた箇所はポイント解説で復習することができます。
※ 一部記述問題などを除く
リスニングは解説動画で
発音の仕方までわかる

 /l/と/r/の発音の仕方
/l/と/r/の発音の仕方
解説動画の中では英語独特の音の発音の仕方や、リズム、音の強弱なども扱います。日本語にはない音の出し方を実践しながら、正しく聞き取る力を養成します。
理由03
もう迷わない!
今週やるべき学習を
ミッションでお知らせ
今週の学習内容が一目でわかるから
自宅学習が習慣になる

新しいスタディサプリはお子さまの学校の進度や学習記録から今やるべき学習を一目でわかるようにまとめたミッション機能を搭載。一週間の学習を「今週のミッション」で提案してくれるので、ミッションにアクセスするだけで迷わず学習を開始できます。また期限内にすべてのミッションの完了を目指すことで理想的なペースで学習を進めることができます。
頑張った分がわかるから
勉強のモチベーションアップ!
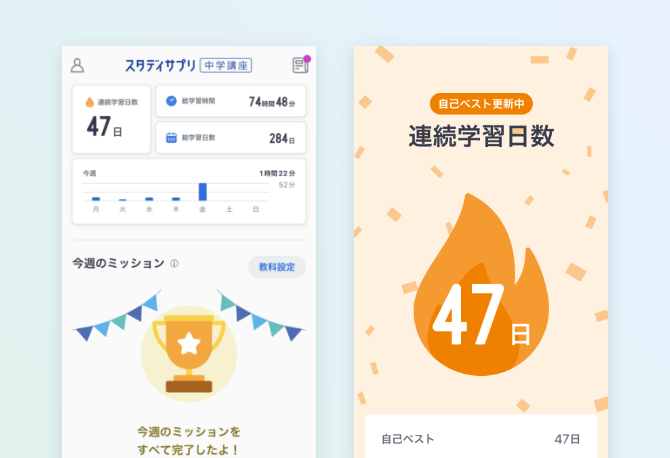
連続学習日数や毎日の学習時間などを可視化。
がんばったことを実感できるとモチベーションアップにつながります。
ミッション機能にも反響続々!
モニター保護者の声
-
ミッション機能でやることに迷わず、すぐに勉強を始められるようになった(中1 保護者)
-
ミッションがあり達成感を感じられるようです(中2 保護者)
理由04
1回5分で集中が途切れない 厳選講師陣による神授業
要点に絞った1回5分※1の集中学習で
学習習慣が身に付く

経験豊富な厳選講師による授業で、学年が上がるごとに難しくなる数学・英語もしっかり理解いただけます。スタサプの授業動画は学校の50分授業の理解するべき要点だけをまとめてプロ講師が5分の神授業に凝縮。カラービジュアルを使ったわかりやすく丁寧な解説で、お子さまを惹きつける工夫がされています。ぜひ、お子さまと一緒にご体験ください。※1※2
※1 教科書対応の基礎力を養成する講座の平均時間から「5分」と表記しています。3〜7分の動画が8割となります。高校受験など応用力を養成する授業動画に関しては、算出母集団に含んでおりません。
※2 スタディサプリは学校の授業で習ったことの復習を前提とし、学校で習う「概念」について大幅に凝縮して要点を説明しているため、学校の授業の予習・復習に効率的にご活用いただけます。
ビジュアルを多くとり入れ
わかりやすくポイントを解説

経験豊富なプロ講師による授業は、カラービジュアルを使ったわかりやすく丁寧な解説で、お子さまを惹きつける工夫がされています。
授業を体験してみる
- 英語
- 数学
- 国語
- 理科
- 社会

 英語
英語
“使える”英語、教えます!
丸岡 幸子まるおか さちこ

 数学
数学
基本に忠実、ユーモア爆発のミスター数学
堺 義明さかい よしあき
堺先生を一番気に入っています。声の抑揚があるので内容に惹き付けられ、要点を問題のたびに繰り返し教えてくれるのでよく頭の中に入ってくるそうです。(中2 保護者)
わかりやすいと言っています。数学の個別塾へ行っているのですが、スタディサプリの方が効率が良い気がすると言っていました。(中3 保護者)

 国語
国語
“国語のわかる”を君にお届け
山下 翔平やました しょうへい
大きなおむすび等の小道具を使ってわかりやすく説明してくれました。(保護者)
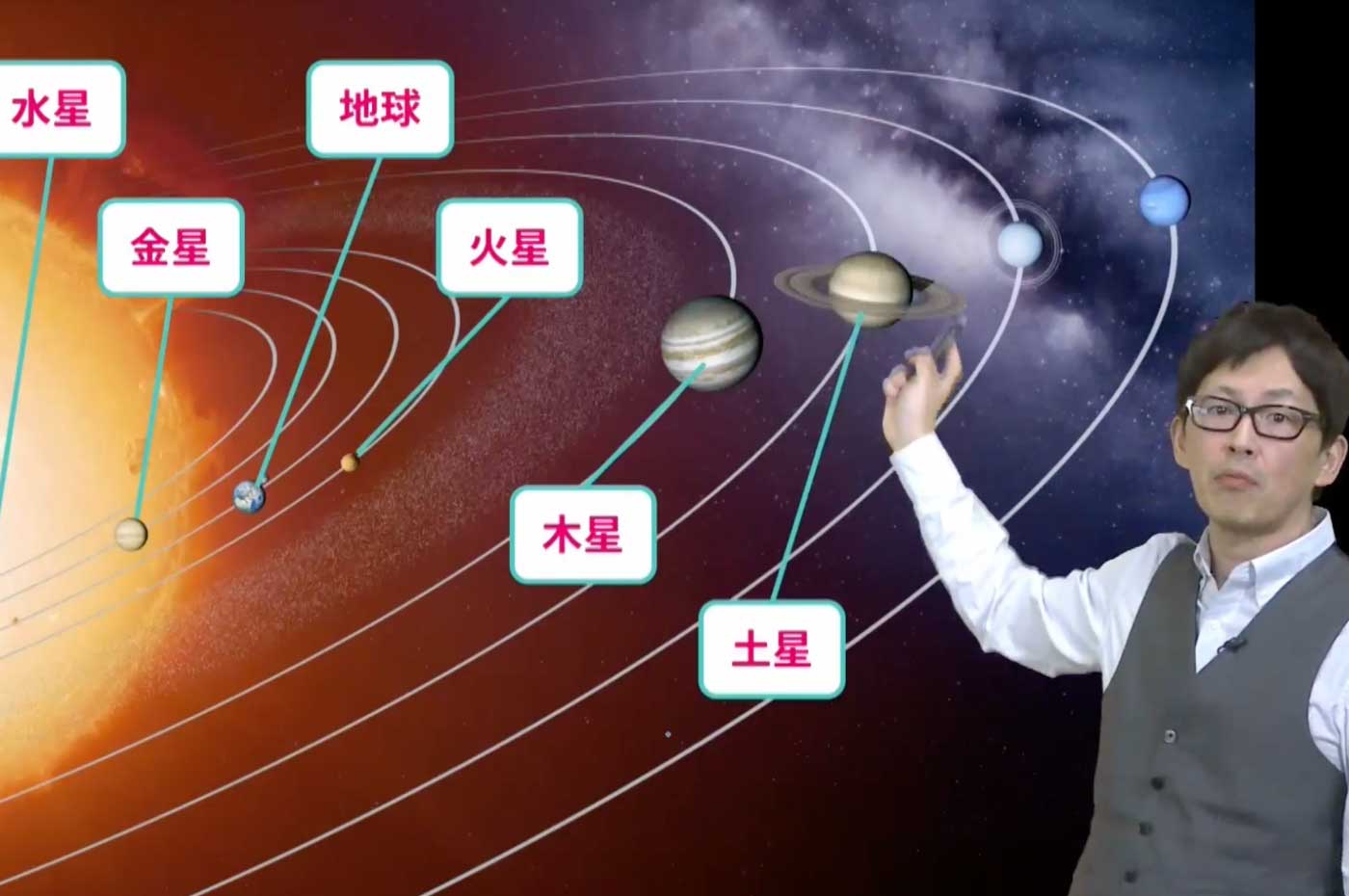
 理科
理科
理科の真髄を伝える関西の本格派
佐川 大三さがわ だいぞう
要点を短い時間で丁寧に解説してくれます。(中3 保護者)
大きなスクリーンに写真や図を出してくれる。また、教える内容と生活を結び付けた例を出してくれるので、理科を身近なものとして考えられるようになったようです。(中3 保護者)

 社会
社会
社会科を爆笑させる風雲児
伊藤 賀一いとう がいち
授業内で、想像しにくいものでも身近な例を挙げているため、より納得しやすいそうです。(中1 保護者)
学校の授業とは全然違うけれど、話が説明的でなく、聞きやすい。一回聞いて要所要所が記憶に残るようです。(中2 保護者)
各教科に精通した厳選講師陣が
お子さまを惹きつけます

スタサプオリジナルテキスト付き
要点を書き込みながら学習できます

授業動画にはオリジナルテキストが付いています。テキストは冊子を購入することも、PDFを無料ダウンロードすることもできるため、学習スタイルにあわせてお選びいただけます。
※ 一部、テキストがない講座があります。
理由05
苦手をつぶす・得意を伸ばす 戻り学習・先取り学習
単元が細かく設定されているので
ピンポイントに学び直しができる
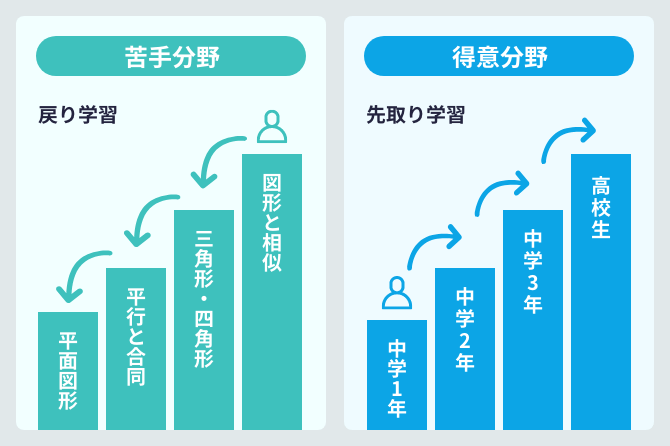
苦手な教科があればさかのぼって戻り学習、得意な教科があればどんどん先取り学習が可能です(小1から高3まで)。授業は各学年の単元ごとに細かくあり、お子さまの理解度に応じてに合わせてピンポイントに学習を進められます。
※小1〜高3までの授業が受講可能です。
※小1~3は、学び直しとして提供しているドリル演習中心の構成です。
レベル別に豊富な 講座ラインナップ
基礎・応用・定期テストから
高校受験対策までを網羅
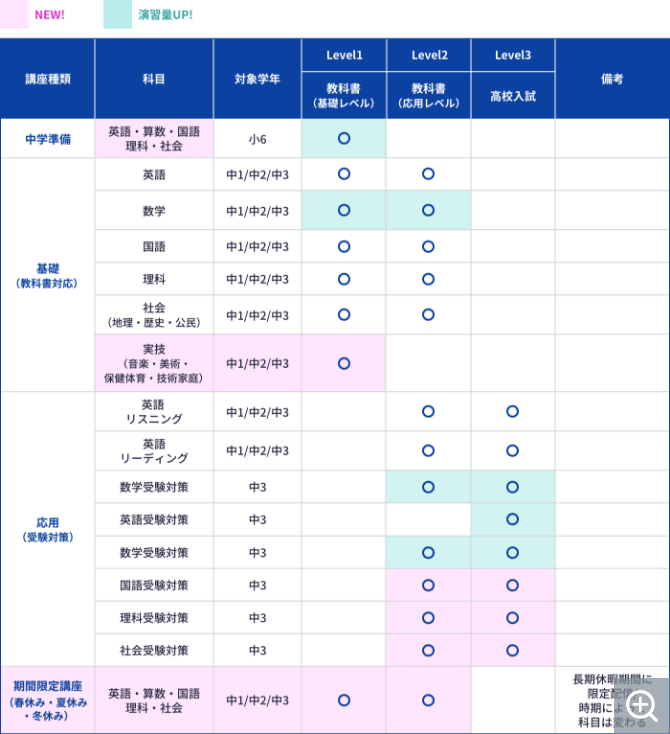
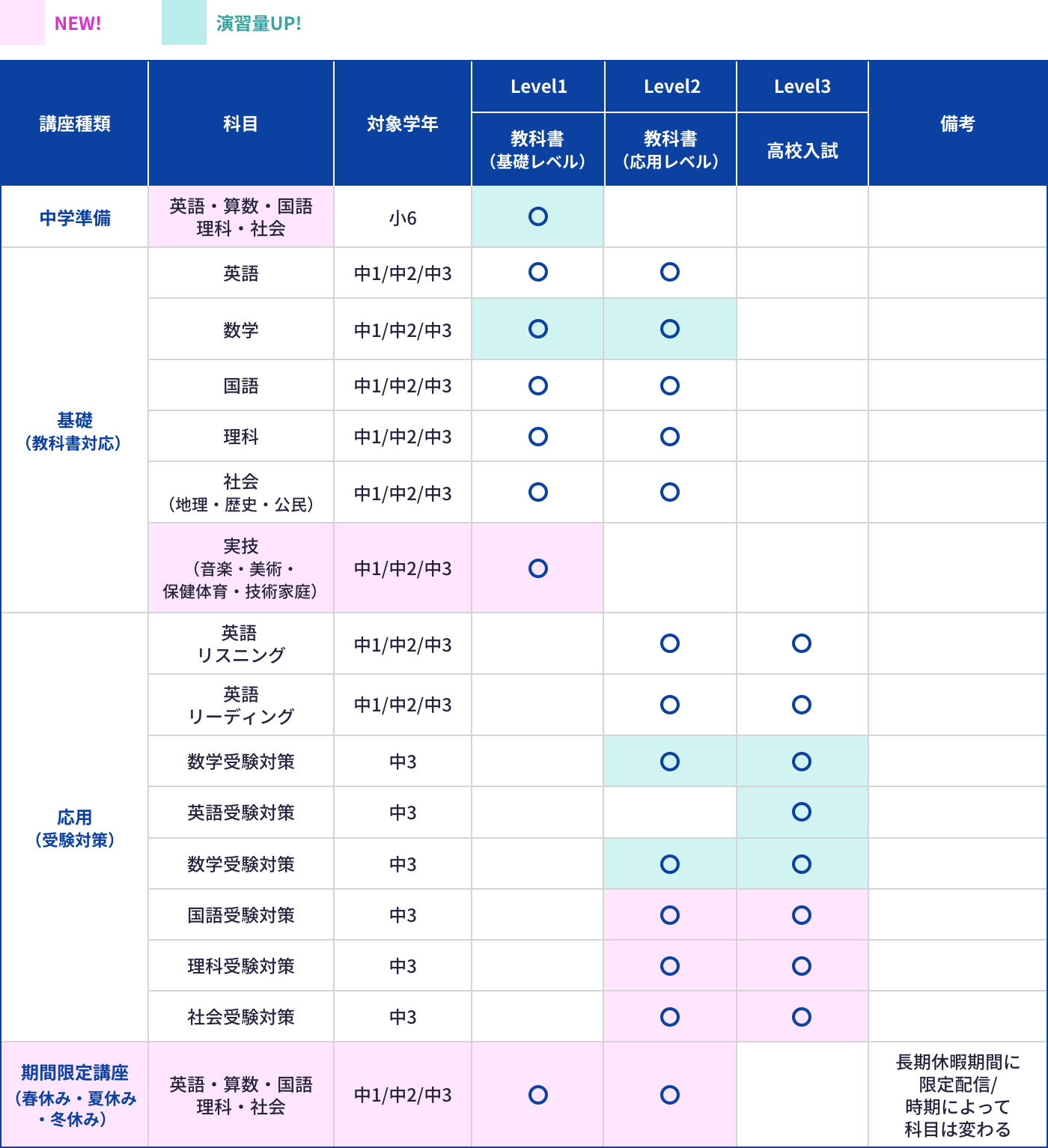
基礎は各学年ごと9教科、応用は受験を見据えて英数を中心にラインナップ。定期テストに出やすい問題を演習する講座や公立高校の過去問を演習する講座など中学3年間をサポートします。
※ 講座の内容は順次追加予定です。リリース情報はこちら
学習進度にピッタリ!
9教科で教科書対応
英語
東京書籍
開隆堂
三省堂
教育出版
光村図書
啓林館
数学
啓林館
東京書籍
学校図書
大日本図書
日本文教出版
数研出版
教育出版
国語
光村図書
理科
東京書籍
啓林館
大日本図書
学校図書
教育出版
社会
東京書籍
(地理・歴史・公民)
帝国書院
(地理・歴史・公民)
教育出版
(地理・歴史・公民)
日本文教出版
(地理・歴史・公民)
山川出版社
(歴史)
育鵬社
(歴史・公民)
音楽
教育芸術社
教育出版
美術
日本文教出版
光村図書
開隆堂
保健
体育
東京書籍
学研
大日本図書
大修館
技術
・
家庭
東京書籍
開隆堂
教育図書
教科書のレベルに応じた講座内容が単元名、順番も教科書どおりに表示されるので、学校の授業進度にそって日々の予習・復習、定期テスト対策を効率的に学習できます。
※ 表に記載されていない教科書をお使いの方は「共通版」講座をお使いください
高校受験にしっかり対応!
受験対策[公立標準・難関]
※ 英数のみ
高校受験を見据えた
ハイレベルな内容を先取り!

※ 数学の例
公立難関高校の合格に向け、応用力を強化できる講座です。英語の長文読解や数学の応用問題など各学年の範囲で解ける入試レベルの演習問題に多く取り組み、応用力を伸ばします。
受験対策実践[公立標準]
公立高校入試問題の出題傾向を分析し
受験に精通したプロ講師が解説!

国語・理科・社会は最新の学習指導要領や出題傾向を踏まえた問題に取り組めます。レベル別の演習問題と授業動画で公立の中堅校から難関校の合格点を目指せます。
※ 47都道府県の出題傾向に合わせた対策講座や、英語・数学は「スタディサプリ 小学/中学/高校/大学受験講座」のWebまたはアプリでご利用いただけます。
※ 数学は各単元の知識事項が関連しているため出題傾向によらず全都道府県で同じ問題を提供しています。
※ 各校独自の入試問題には対応しておりません。別途、過去問などで対策が必要です。
スタディサプリ中学講座 その他の特長
本当に勉強できているのか心配…
お子さまの学習状況を見守る
保護者メール
お子さまの学習進捗を
メールで確認できます

毎日「勉強したの?」を聞くのは保護者の方に大きな負担になるもの。学習時間や受講講座ごとの正答率などをメールでお届けします。1週間まとめた視聴状況も見られるので学習の波もわかります。またお子さまの学習画面上でリアルタイムで確認もできます。お子さまの学習習慣の基礎をつけるためにご活用ください。
※ まなレポは、保護者用の管理画面からもご確認いただけます。
専用端末不要
自宅のスマホやタブレットで
1回約5分の集中学習

何かと忙しい中学生でもちょっとしたスキマ時間を利用して学習が可能。スマホを利用すれば移動中でも授業動画や演習問題にアクセスできます。
定期テスト前にはタブレットやパソコンを利用して、テキストを見ながらじっくり学習に取り組むこともできます。
勉強を頑張った分、
やる気が高まる楽しい仕組み

サプモン
勉強してコインを貯めると、オリジナルキャラクターの洋服を着せ替えることができたり、部屋をカスタマイズしたり、自分専用のペット「サプモン」にえさをあげて育成するなどゲーム感覚で楽しめます。
ベーシックコース料金
ベーシックコース1か月無料キャンペーン 期間| 2024/4/1 (月) 0:00 ~ 2024/4/25 (木) 16:59 まで
クレジットカード決済限定
※コンビニ決済、App Store決済、Google Play Store決済でのお申し込みは対象外です。
14日間以内に利用停止手続きをすれば料金は一切不要!
申し込めばすぐ授業視聴可能です
※ 14日間には「受講申し込み日」を含みます。
※ 14日間無料体験はWebサイト、かつクレジットカード決済での受講申し込み手続きをされた場合のみに適用されます。
個別指導塾オンライン
こんな方におすすめ!
- 個別に指導して
もらたい - 質問や相談が
したい - 塾とお悩みの方
コース・料金比較
14日間無料体験実施中!
入会金・初期費用は一切不要
前提となります。
- 特長
-
今週の学習内容が
一目でわかるミッション機能で
迷わず学習
-
個別指導塾オンライン 週1回60分 先生と話せる
オンラインでの個別指導
- こんな方におすすめ!
-
- 通信教育とお悩みの方
- 自分のペースで勉強したい
- 月々の負担を減らしたい
-
- 塾とお悩みの方
- 個別に指導してもらいたい
- 質問や相談がしたい
- 通常料金
-
12か月
一括払い月払い
月額2,178\
-
月額10,780\
(内訳)
ベーシック
+
個別指導塾オンライン - 無料体験期間
-
14日間
※ クレジットカード決済の場合のみ
※ 無料体験期間は登録日から起算して14日間です - 比べてお得!
(月払いの場合) -

-

- 備考
-
※ 個別指導塾オンラインの対象は公立中学校の定期テストで点数アップを目指す方となります。
※ 出典:「子供の学習費調査(令和3年度文部科学省)」より中学校 通信教育・家庭教師費(支出者平均額)と学習塾費(支出者平均額)に「学校基本調査(令和4年度文部科学省)」公立・私立の児童数を加重平均し月額に加工して算出。
学校向けサービスと個人向けサービスの違いについて
※ 本ページで説明している個人向けサービスと学校向けサービスとでは提供するサービス内容が異なります。家庭学習は新機能を含む個人向けサービスのご利用がおすすめです。
サービスの違いについての詳細はこちらをご参照ください。
ベーシックコース1か月無料キャンペーン 期間| 2024/4/1 (月) 0:00 ~ 2024/4/25 (木) 16:59 まで
クレジットカード決済限定
※コンビニ決済、App Store決済、Google Play Store決済でのお申し込みは対象外です。
14日間以内に利用停止手続きをすれば料金は一切不要!
申し込めばすぐ授業視聴可能です
※ 14日間には「受講申し込み日」を含みます。
※ 14日間無料体験はWebサイト、かつクレジットカード決済での受講申し込み手続きをされた場合のみに適用されます。





しゃべるスピードがちょうど良く、大事なところは繰り返し言ってくれるので、学校でわからなかったところがわかるようになった。(中2 保護者)
ハーイゼア!から始まる授業は、わかりやすくて聞きやすいようです。明るいお姉さんで、ポイントの説明が素晴らしいです。(中1 保護者)